Sabtu, 26 September 2015

PID controller theory

06.31 Unknown


The PID control scheme is named after its three correcting terms, whose sum constitutes the manipulated variable (MV). The proportional, integral, and derivative terms are summed to calculate the output of the PID controller. Defining u(t) as the controller output, the final form of the PID algorithm is:
\mathrm{u}(t)=\mathrm{MV}(t)=K_p{e(t)} + K_{i}\int_{0}^{t}{e(\tau)}\,{d\tau} + K_{d}\frac{d}{dt}e(t)
where
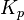K_p: Proportional gain, a tuning parameter
K_i: Integral gain, a tuning parameter
K_d: Derivative gain, a tuning parameter
e: Error = SP - PV
t: Time or instantaneous time (the present)
\tau: Variable of integration; takes on values from time 0 to the present t.
Equivalently, the transfer function in the Laplace Domain of the PID controller is
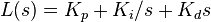
L(s)=K_p + K_{i}/s + K_{d}s
where
s: complex number frequency
Posted in Automation

Langganan: Posting Komentar ( Atom )
Twitter Delicious Facebook G+ Arduino Favorites More
RSS Feed Subscribe to Our RSS feed!
Follow Us on Twitter! Follow Us on Twitter!