PID CONTROLLER

A proportional-integral-derivative controller (PID controller) is a control loop feedback mechanism controller commonly used in industrial control systems. A PID controller continuously calculates an "error value" as the difference between a measured process variable and a desired setpoint. The controller attempts to minimize the error over time by adjustment of a control variable, such as the position of a control valve, a damper, or the power supplied to a heating element, to a new value determined by a weighted sum:

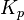where , , and , all non-negative, denote the coefficients for the proportional, integral, and derivative terms, respectively (sometimes denoted P, I, and D). In this model, P accounts for present values of the error (e.g. if the error is large and positive, the control output will also be large and positive), I accounts for past values of the error (e.g. if the output is not sufficient to reduce the size of the error, error will accumulate over time, causing the controller to apply stronger output), and D accounts for predicted future values of the error, based on its current rate of change.

As a PID controller relies only on the measured process variable, not on knowledge of the underlying process, it is a broadly useful controller. By tuning the three parameters of the model, one can design a PID controller for specific process requirements. The response of the controller can be described in terms of the responsiveness of the controller to an error, the degree to which the controller overshoot the setpoint, and the degree of system oscillation. Note that the use of the PID algorithm for control does not guarantee optimal control of the system or system stability.
Some applications may require using only one or two terms to provide the appropriate system control. This is achieved by setting the other parameters to zero. A PID controller will be called a PI, PD, P or I controller in the absence of the respective control actions. PI controllers are fairly common, since derivative action is sensitive to measurement noise, whereas the absence of an integral term may prevent the system from reaching its target value due to the control action.
For the discrete time case, the term PSD, for proportional-summation-difference, is often used.